개발 원조의 비리를 찾아내기

개발 원조의 비리를 찾아내기

Detecting Fraud in Development Aid

by Jean Ensminger and Jetson Leder-Luis (NBER wp#30768)

위 페이퍼를 정리하기 전에 벤포드 법칙(Benford’s Law)이라는 걸 소개해야 할 듯 하다. 벤포드 법칙은 넓은 분포를 가지는 수치 데이터들의 제일 앞자리 숫자가 작은 숫자인 경향을 보인다는 것이다.

(여기서 넓은 분포를 가진다는 거는 데이터가 1->2->3이렇게 선형으로 변하는 게 아니라, 1->2->4->8 이런식으로 배율로 변하는 데이터를 가진다는 걸 뭉뚱그려 표현한 것임. 반대로 말하면, 데이터가 배율로 증가하는 거면, log변환을 해서 선형증가를 보여주는 게 좋을 법한 데이터들이 벤포드 법칙을 따를만한 적절한 데이터라는 것임. 예를 들어 주식가격의 경우, 100원짜리 주식이 150원으로 50%나 상승하는 거는 힘든 일이지만, 10만원짜리 주식이 10만 50원이 되는 건 눈 깜짝할사이에도 일어날 수 있는 걸 생각해보면, 데이터의 변화가 선형 level이 아니라 비율로 변화하는 자료인 경우라 벤포드 법칙이 성립하기 좋을 수 있는 데이터임)

자연적으로 생성되는 데이터는 벤포드 법칙을 따르기 좋다는 걸 확인하기 위해 피보나치 수열의 제일 앞자리 숫자 빈도와 벤포드 법칙의 분포를 아래 코드를 통해 찍어보니, 관측 수가 몇 개 되지 않는데도 잘 비슷한 걸 확인할 수 있음.

## illustration을 위한 Python code.
import math
import matplotlib.pyplot as plt
obs=1000 #관측수
X=[0]*obs #append하는것보다 빈 리스트 만들어 놓는게 사소하게 빠름
Y=[0]*obs
#피보나치 수열 생성
for i in range(obs):
    if i<2:
        X[i]=1
        Y[i]=1
    else:
        X[i]=X[i-1]+X[i-2]
        Y[i]=int(str(X[i])[0]) #제일 앞자리수
#각 앞자리수 빈도 구하기
freq=[0]*9
for i in range(obs):
	for j in range(9):
		if Y[i]==j+1:
			freq[j]+=1
ratio = [f/obs for f in freq]
benford = [math.log10(1+1/d) for d in range(1,10)]
plt.plot(range(1,10), benford, 'r--', range(1,10), ratio, 'bs')
plt.show()

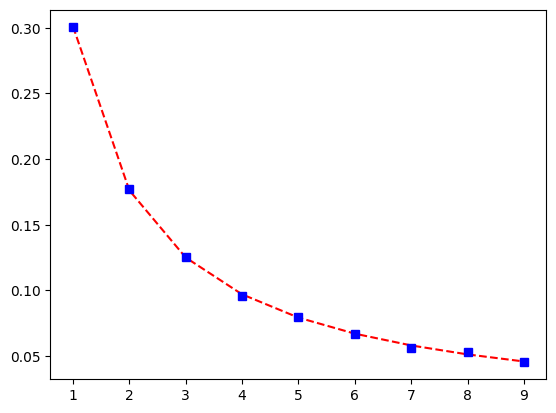
(위 그림에서 빨간 점선이 벤포드 법칙을 나타내는 선이고, 파란 네모가 실제 1000개의 피보나치 수열의 숫자 앞자리의 상대적 빈도임)

이걸 왜 이렇게 길게 얘기했냐면, 데이터 조작 여부를 벤포드 법칙을 따르는 지 확인하는 것으로 테스트할 수 있기 때문이다. 예를 들어, 트위터 사용자의 친구의 친구 숫자가 벤포드 법칙을 따르는 것을 알고 있다면, 이를 따르지 않는 소수의 이상한 계정은 ‘트윗봇’ 계정일 확률이 높다는 걸 알려준다.

위에 언급한 연구는 저개발국가를 원조해주는 과정에서 조작이 없었는지를 확인하는 연구다. 월드뱅크가 케냐에 원조를 한 프로젝트들에 리포트된 숫자들이 얼마나 벤포드 법칙에서 벗어나는지 확인해보니, 자금 관리의 투명성이 약한 섹터나, 선거가 있는 해에 데이터 조작이 더 크게 일어난다고 해석할 수 있는 관찰을 함.